[OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문] 챕터 4 - 좌표계와 변환

• 게임과 같은 3차원 가상 공간은 많은 물체들로 구성되어 있는데, 각 물체의 위치는 이동(translation)에 의해, 방향은 회전(rotation)에 의해 결정된다. 또한 각 물체는 축소확대(scaling)될 수도 있다.
• 이러한 이동, 회전, 축소확대를 총칭하여 변환(transform)이라고 한다.

 

 

---

 

4.1 2차원 변환의 행렬 표현

4.1.1 축소 확대

2차원 벡터(x,y)는 행렬-벡터 곱셈을 통해 축소, 확대된다.

 

4.1.2 회전

2차원 벡터 p는 원점을 기준으로 ∂만큼 회전하여 p'가 된다. 벡터 p의 길이가 r이라면 p의 좌표는 다음과 같다.

삼각함수의 덧셈 정리가 사용된다.

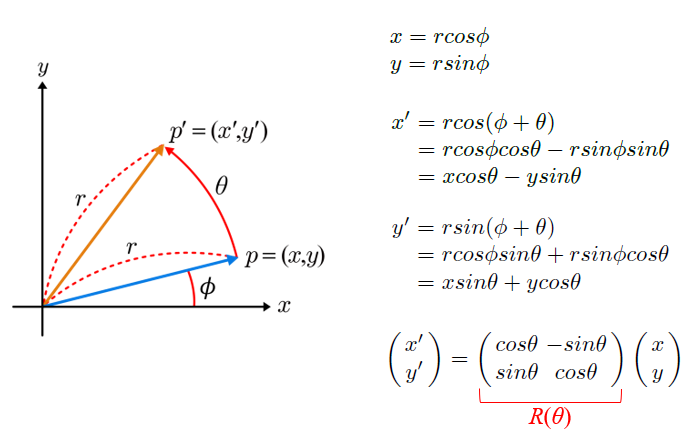
• 시계방향으로의 회전 행렬을 얻으려면 R(∂)에 ∂대신 -∂를 넣으면 된다.
• -∂만큼 회전은 2π-∂만큼 회전하는 것과 동일하다.

 

 

4.1.3 이동과 동차 좌표

• 축소확대와 회전은 이른바 선형 변환(linear transform)이라는 범주에 속한다.
• 축소확대와 회전 말고도 컴퓨터 그래픽스에서 자주 사용되는 또 다른 변환은 이동(translation)이다.
• (x, y)에 놓인 점을 (x+dx, y+dy)로 이동시키는데, (dx, dy)를 변위 벡터(displacement vector)라고 부른다.
• 이동은 선형 변환의 범주에 속하지 않으며, 벡터 덧셈으로 구현된다.

이동은 벡터 덧셈으로 구현된다.

• 이는 행렬 곱셈으로 구현되는 축소확대 및 회전과 다르다. 하지만, 동차좌표(homogeneous coordinates)를 사용하면, 이동 역시 행렬 곱셈으로 구현될 수 있다.
• 한 점의 2차원 카테시안 좌표(x, y)가 주어질 때 이에 대한 동차 좌표는 간단히 (x, y, 1)로 표현할 수 있다.
• 3 X 3 단위 행렬의 마지막 열에 아래처럼 (dx, dy)를 삽입하면, 이것이 바로 이동 행렬이 된다.

(2, 3, 1)과 원점을 지나는 직선은 무한히 많은 동차 좌표들의 집합이다.

• 하나의 동차 좌표를 카테시안 좌표로 바꾸려면 이 직선을 따라 w = 1 평면으로 투영(project)시키면 된다.
• 동차 좌표는 (x, y, 1)로 국한되지 않는다. 대신, (wx, wy, wz)로 표현된다. 단, w는 0이 아니어야 한다.
• 2차원을 구성하는 x축과 y축에 w축이 추가되어 3차원 공간을 만들었는데, 원점을 지나는 3차원 직선은 카테시안 좌표 (2,3)에 해당하는 무한히 많은 동차 좌표들이 모인것으로 보면 된다.

동차 좌표를 다루기 위해 축소확대 및 회전의 2x2 행렬 형태를 변경한 모습

 

 

---

 

 

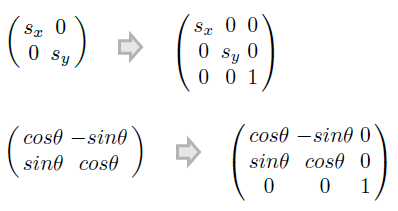
4.1.4 2차원 변환의 결합

2차원 변환의 결합

• 행렬 곱셈에서는 교환 법칙이 성립하지 않는다.
• 앞의 회전은 원점을 중심으로 한 것이다. 임의의 점을 중심으로 하는 회전에 대해서는 먼저 원점으로 옮긴 후 회전을 시키고 다시 이동을 시켜주면 된다.

1. (x, y)를 (-a, -b)만큼 이동
2. 이동된 점(x-a, y-b)를 원점 중심으로 회전
3. 회전 결과를 (a, b)만큼 이동

 

 

---

 

 

4.2 아핀 변환

• 축소확대, 회전, 이동의 세 변환 중, 축소확대와 회전은 선형 변환 범주에 속하지만, 이동은 그렇지 않다. 선형변환과 이동을 포함하는 범주를 아핀 변환(affine transform)이라 한다.
• 2차원 아핀 변환은 3x3 행렬로 표현되므로, 몇 개의 아핀 변환이 주어지건 이는 모두 하나의 행렬로 결합 가능하다.

회전(R)에 이은 이동(T)이 결합된 행렬 + 축소확대(S)를 추가

• 행렬의 3번 행은 항상 (0 0 1)로 고정된다는 것
• 이렇게 고정불변인 3번 행을 무시하고 나머지 2x3 행렬을 [L | t]로 표기하자. L은 왼쪽의 2x2 행렬을, t는 3번열을 말한다.
• 여러 개의 아핀 변환이 결합된 [L | t]에서, L은 '누적된 선형 변환'을, t는 '누적된 이동'을 표현한다.
• [L | t]로 변환하는 것을 개념적으로 해석하면, 그 물체에 L을 먼저 적용하고 그렇게 선형 변환된 물체에 t를 적용하는 것과 같다. 즉, 폴리곤 메시로 표현된 물체의 각 정점을 p라 할 때, Lp + t 방식으로 변환이 이뤄지는 것이다.

 

• 축소확대 없이 회전과 이동이 결합된 변환을 생각해보자. 이 변환은 물체의 방향과 위치를 변경시킬 뿐 그 물체의 외양에는 영향을 미치지 못한다.
• 이런 점에서 이를 강체 변환(rigid motion)이라 부른다.

 

 

---

 

 

4.3. 3차원 변환의 행렬 표현

• 2차원 아핀 변환과 크게 다르지는 않은 3차원 행렬 표현이다.

 

4.3.1 축소확대

3차원 축소확대 (균등 / 비균등)

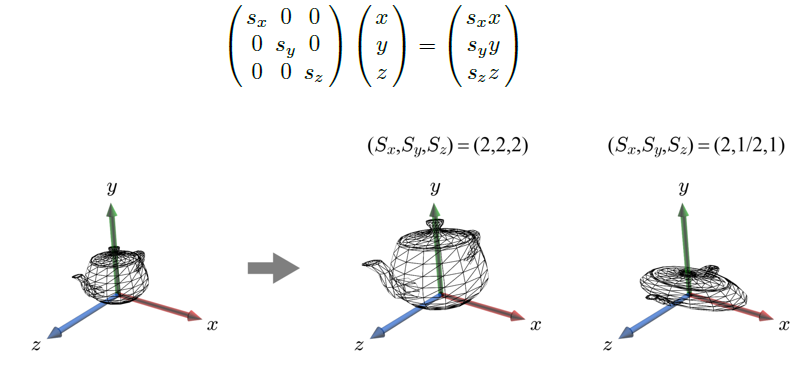
• 모든 축소확대 인자가 같으면 균등(uniform)하다고, 그렇지 않다면 비균등(non-uniform)하다고 부른다.

 

 

4.3.2 회전

• 회전 중심을 필요로 했던 2차원 회전과는 달리, 3차원 회전은 회전축(axis of rotation)을 필요로 한다.
• z축을 중심으로 ∂만큼 회전하는 Rz(∂)를 유도하면, 이 벡터의 z좌표는 Rz(∂)에 의해 바뀌지 않는다.

z축 중심 회전

• 한 물체를 z축 중심으로 ∂만큼 회전시키려면, 그 물체의 폴리곤 메시를 구성하는 모든 정점에 Rz(∂)를 적용한다.

 

x축 중심 회전

• Rx(∂)는 x좌표를 바꾸지 못한다.

y축 중심 회전

• y축 중심 회전도 마찬가지다.

 

회전 방향에 대한 부호 변경

• 회전이 반시계 방향으로 이뤄지는 것으로 보이면 회전 각도 ∂는 양수가 되고, 반대로 회전이 시계방향으로 이뤄지면 ∂는 음수가 된다.

 

 

---

 

 

4.3.3 이동과 동차 좌표

• 동차 좌표를 이용한 3차원 이동은 4x4 단위 행렬의 마지막 열에 (dx, dy, dz)를 삽입한 것으로 정의된다.

동차좌표를 이용한 3차원 이동

동차 좌표를 이용한 3차원 축소확대

 

 

---

 

 

4.4 월드 변환

자신의 오브젝트 공간에서 정의된 구와 주전자가 월드 공간으로 모아진다.

• 하나의 물체를 모델링하는 데 사용된 좌표계를 오브젝트 공간(object space)이라 부른다.
• 각자의 오브젝트 공간에서 정의된 물체들로 3차원 가상 환경을 구성하려면 이들을 하나의 좌표계로 통합해야 하는데, 이 좌표계를 월드 공간(world space)이라 부른다.
• 그림과 같이 각각의 구와 주전자를 만들고 월드 변환(world transform)을 통해 월드 공간으로 옮겨진다.
• 이 과정에서 앞서 말한 아핀 변환의 모든 것이 적용된다.
• 2차원 아핀 변환의 특성은 3차원에서도 그대로 유지되며, 행렬 곱셈에서는 교환 법칙이 성립하지 않는다.

 

 

---

 

 

4.5 회전과 오브젝트 공간 기저

• 오브젝트 공간에서 한 물체의 모델링이 완료되면, 그 물체는 자신의 오브젝트 공간과 일체가 된다. 즉, 물체를 움직이게 되면 그 오브젝트 공간도 따라서 같이 움직인다.

한 물체의 오브젝트 공간 기저는 그 물체의 방향을 표현한다.

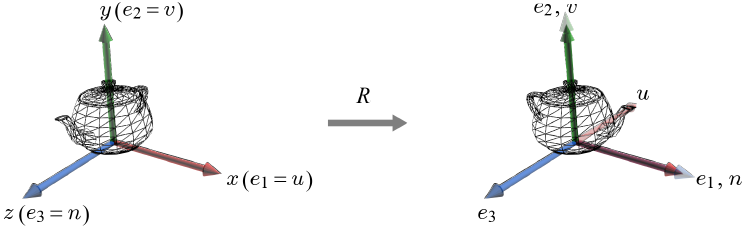
• (e1, e2, e3)는 월드 공간의 기저를, (u, v, n)은 오브젝트 공간의 기저를 나타낸다.
• 초기에 그 둘은 일치하지만, 물체가 회전하며, 오브젝트 공간 기저 (u, v, n)은 (e1, e2, e3)와 다르게 된다. → 회전 후 물체의 방향은 (u, v, n)으로 표현할 수 있다.

e1과 회전(R)의 관계

e2와 회전(R)의 관계, e3와 회전(R)의 관계

R은 다음과 같이 정리된다.

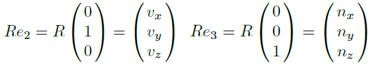
• 예시에서 확인할 수 있듯, 회전된 물체의 오브젝트 공간 기저인 (u, v, n)이 주어졌다면, 그 회전 행렬을 즉각 정의할 수 있다. 즉, (u, v, n)으로 세 열을 채우면 된다.

 

 

---

 

 

4.6 역변환

• 컴퓨터 그래픽스에서 역변환(inverse transfrom)은 매우 자주 사용되는 개념이다.
• 변위 벡터가 (dx, dy, dz)인 이동 T의 역변환은 (-dx, -dy, -dz_)만큼 이동하는 것이다.

  

  

  T와 T의 역변환, T의 역행렬

 

• 회전의 역변환을 정의해 보자. 우리는 항상 오브젝트 공간 기저 (u, v, n)이 직교 정규 성질을 가진다고 가정한다.
• 따라서, 하나의 기저 벡터가 자신과 내적되었을 때 그 결과는 1이다. 반면, 서로 다른 기저 벡터 간 내적은 0이 된다.

 

회전행렬과 그 전치행렬의 곱을 정리

• 회전의 전치행렬을 취하면 바로 역변환을 얻게 된다.

 

역회전

 

 

---

 

 

출처

[OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문]을 보고 공부하고 정리한 내용입니다.