[OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문] 챕터 3 - 모델링

 

 

• 3차원 물체를 표현하는 다양한 기법이 존재하지만, 실시간 그래픽스 영역에서는 폴리곤 메시를 압도적으로 많이 사용한다.

 

 

---

 

3.1 폴리곤 메시

구를 표현하는 두 가지 기법, 음함수 곡면과 폴리곤 메시

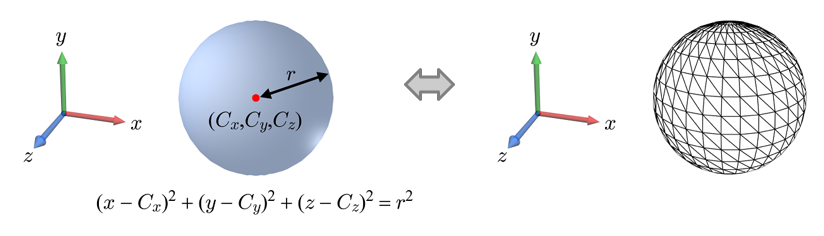
• 오른쪽 그림, 폴리곤 메시와 같이 정점(vertex) 및 폴리곤과 같은 요소들을 명시적으로 정의하여 구를 표현할 수 있다.
• 게임을 비롯한 실시간 응용에서는 폴리곤 메시를 선호하는데, 그 이유는 GPU가 폴리곤 메시 처리에 최적화되어 있기 때문이다.
• 하지만, 폴리곤 메시는 정확한 표현법이 아닌 근사적 표현법이라는 사실을 염두해 두자.

 

삼각형 메시와 사각형 메시

• 가장 간단한 폴리곤은 삼각형이다. 폴리곤 메시 중 가장 널리 쓰이는 것은 삼각형으로만 구성된 메시, 즉 삼각형 메시(triangle mesh)이다.
• 하지만 모델링 작업을 위해서는 사각형 메시(quad mesh)가 선호된다.
• 사각형 메시가 주어졌을 때 이를 삼각형 메시로 바꾸는 가장 간단한 방법은, 각 사각형을 두 개의 삼각형으로 분할하는 것이다.

 

Human Head Modeling [HD] : 牛山雅博

Level Of Detail (LOD)

• 폴리곤 메시는 부드러운 곡면을 근사적으로 표현한 것이다. 따라서 얼마나 많은 정점을 사용하여 근사할 것인가는 중요한 문제가 된다.
• 정점 개수가 많으면 메시의 해상도(resolution)가 높다고 말하며, 정점이 적으면 해상도가 낮다고 표현한다.
• 그림과 같이 해상도는 정확성과 효율성 사이의 상반관계를 고려하여 결정된다.
• 메시의 해상도가 올라갈수록 본래의 곡면과 흡사해지지만 메시를 처리하기 위한 시간이 증가하여 효율성은 떨어진다.

 

 

---

 

 

3.1.2 폴리곤 메시 표현

삼각형 메시 표현. 인덱스를 사용하지 않는 경우, n개의 삼각형을 가진 폴리곤 메시를 표현하기 위해서는 정점 배열에 3n개의 정점이 저장되어야 한다.

• 삼각형 메시를 표현하는 가장 단순한 방법은 삼각형을 구성하는 세 개의 정점을 순서대로 나열하는 것, 한 번에 세 개씩 정점을 읽어서 하나의 삼각형을 정의한다.
• 정점들이 저장된 메모리 공간은 정점 배열(vertex array)이라 부른다.
• 이 표현법은 상당히 직관적이지만, 중복된 데이터를 가진다는 단점이 있다.

 

삼각형 메시 표현, 중복된 정점이 없는 정점 배열을 만들고, 인덱스 배열을 사용한다.

• 정점 배열에는 정점들을 중복없이 저장하고, 이들을 가리키는 인덱스를 별도의 인덱스 배열(index array)에 기록하면 효율적으로 메모리를 사용할 수 있다.
• 정점 배열(vertex array)에는 일반적으로 정점 위치뿐만 아니라 다종다양한 데이터가 포함된다.
• 중복된 데이터를 제거하여 절약되는 정점 배열 공간은 인덱스 배열이 차지하는 공간 크기를 능가하게 된다.

 

 

---

 

 

3.2 표면 노멀

• 3차원 물체를 렌더링할 때 핵심적인 역할을 하는 것은 그 물체 표면의 노멀(surface normal), 즉 표면에 수직인 법선 벡터이다.

 

3.2.1 삼각형 노멀

삼각형 노멀, 세 개의 정점 P1, P2, P3로 구서오딘 삼각형, 삼각형 노멀은 벡터곱 v1 x v2로 정의된다.

• 삼각형 노멀은 벡터곱 v1 x v2로 정의되며, 오른손 법칙이 적용된다.
• 삼각형의 정점 순서가 <P1, P2, P3>일 경우 다음과 같이 삼각형 노멀이 정의된다. (반시계 방향)

 

삼각형의 순서가 <P1, P3, P2>순으로 되어있다면

• 다음과 같은 순서를 거치게 되면 앞서 보았던 삼각형 노멀 방향과는 반대의 결과가 나오게 된다.
• <P1, P2, P3>와 <P1, P3, P2>는 같은 삼각형은 맞지만 바깥으로 나가는 노멀과 안으로 향하는 노멀로 나오게 된다.
• 컴퓨터 그래픽스에서는 모든 노멀이 물체 바깥으로 향하게 하는 것이 원칙이다. 따라서, 삼각형의 정점은 항상 반시계 방향으로 정렬되어 있어야 한다.

 

정점 노멀. 정점 노멀은 해당 정점이 샘플한 곡면의 노멀을 표현한다. 정점 노멀은 해당 정점을 공유하는 삼각형들의 노멀 평균으로 정의할 수 있다.

• 시작점은 그렇게 중요하지는 않다. 대신, 반시계방향으로 통일하기

 

 

---

 

 

3.2.2 정점 노멀

 

정점 노멀. 정점 노멀은 해당 정점이 샘플한 곡면의 노멀을 표현한다.

정점 노멀은 해당 정점을 공유하는 삼각형들의 노멀의 평균으로 정의할 수 있다.

• 컴퓨터 그래픽스에서 실제 중요한 것은 정점 노멀(vertex normal)이다.
• 생각해보면, 원래 부드러운 곡면을 샘플하여 폴리곤 메시의 정점을 얻은 것이다. 정점 노멀은 해당 정점이 샘플한 곡면에 수직이어야 함을 이해할 수 있을 것이다.
• 하지만, 원래의 곡면(smooth surface)없이 폴리곤 메시만 주어졌을 때 정점 노멀을 계산하는 정답은 없다. 그럴듯한 결과를 내는 기법들이 사용될 뿐이다.
• 가장 간단한 방법은 그림과 같이 하나의 정점을 공유하는 모든 삼각형 노멀들의 평균을 취하는 것이다.
• 정점 노멀은 3ds Max 등과 같은 패키지가 자동으로 계산한다. 정점 노멀은 라이팅에 필수적이므로, 정점 위치와 더불어 정점 배열의 핵심 구성 요소가 된다.

 

 

---

 

 

3.3 폴리곤 메시 내보내기와 불러오기

• 하나의 응용프로그램에서 만들어진 데이터를 다른 응용프로그램에 적합한 형태로 출력하는 과정은 내보내기 혹은 익스포트(export)라 부르고, 이렇게 출력된 데이터를 읽어오는 과정은 불러오기 혹은 임포트(import)라 한다.

 

application 1 : 3ds Max, Maya ... / application 2 : unity ...

• 3ds Max가 지원하는 대표적인 파일 포맷 중 하나는 .obj이다.
• 이는 기본적으로 정점 위치와 노멀, 그리고 삼각형 정보를 저장하는데, 정점 위치는 vertex의 앞으로 v, 정점 노멀은 vertex normal의 앞 글자 vn, 삼각형은 face(면)의 앞 글자 f를 기호로 사용한다.

v는 정점 위치, vn은 정점 노멀, f는 삼각형 정보 (export)

• 구의 경우 특별한 경우라 vertex normal이 각각 고유하기 때문에 많은 vertex normal을 가지게 된다.

vertex array에는 임포트한 내용에서 삼각형 정보를 가져와 vertex와 vertex normal을 채워 넣어 준다. (import)

• 내보내기(export)한 모델링의 삼각형 개수는 48개이니까, 불러오기(import)한 index array에는 48x3 = 144개 만큼의 배열이 필요하다.

 

 

---

 

 

출처