[Open GL ES를 이용한 3차원 컴퓨터 그래픽스 입문] 챕터 11 - 오일러 변환 및 쿼터니언 [1/2]

 

 

 

• 4.3.2절에서 우리는 x, y, z축을 중심으로 하는 세 종류의 회전을 소개했다.
• 이 장은 그러한 회전을 적절하게 결합하면 물체가 임의의 방향을 가지게 됨을 보여줄 것이다.
• 그 다음 주축이 아닌 임의의 축을 중심으로 물체를 회전하는 기법에 대해 기술할 것이다.

 

 

 

---

 

 

 

11.1 오일러 변환

 

• 세 개의 주축 중심 회전을 결합한 것을 오일러 변환(Euler transform)이라 한다. 그런데, 이 주 축은 월드 공간에서 택할 수도 있고, 오브젝트 공간에서 택할 수도 있다.

 

11.1.1 월드 공간 오일러 변환

 

월드 공간 오일러 변환. x, y, z축 순서 회전

월드 공간 오일러 변환. y, x, z축 순서 회전

 

위의 그림의 회전을 다음 행렬 식으로 표현할 수 있다.

 

 

 

---

 

 

 

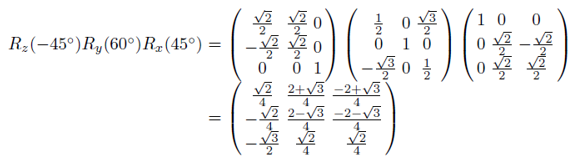
11.2 키프레임 애니메이션과 오일러 변환

 

11.2.1 2차원 키프레임 애니메이션

 

키프레임의 위치와 방향이 보간되어 중간 프레임을 결정한다.

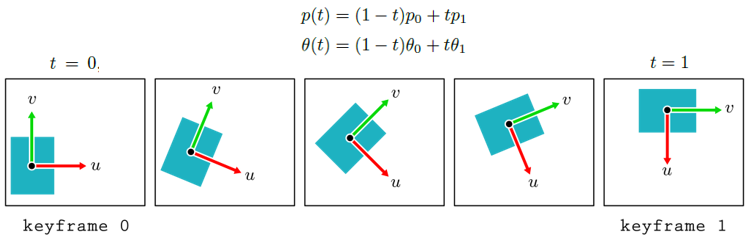
• p_i는 사각형 중심의 좌표를, ∂_i는 회전각 즉 방향을 나타낸다.
• 중간 프레임 t에서의 사각형의 위치는 위의 식과 같이 선형보간을 통해 결정된다.
• 사각형의 방향도 아래식과 같은 방식으로 선형보간된다.

 

 

 

 

 

11.2.2 3차원 키프레임 애니메이션

 

• 2차원 키프레임 애니메이션에서 소개한 개념은 3차원에 그대로 적용된다.

 

3차원 키프레임 애니메이션은 2차원 키프레임 애니메이션과 개념적으로 동일하다. 키프렝미의 위치와 방향이 보간되어 중간 프레임을 결정한다.

 

 

• 오른쪽 그래프는 x, y, z축 중심의 회전 각도를 보여주는데, 이는 바로 오일러 각이다.
• 좌측 열의 세 그래프는 이러한 오일러각 및 그 선형보간 결과를 보여준다.

 

부드러운 애니메이션은 종종 고차원 보간을 통해 얻어진다.

 

 

• 앞서 나온 선형보간 대신 고차원 보간을 선택할 수도 있고 다음 그림과 같이 보간 곡선의 모양을 변경할 수도 있다.

 

 

 

11.2.3 오일러 각의 보간

 

오일러 각은 임의의 방향을 표현하는 데 자주 사용되지만, 때로 올바르게 보간되지 않는다는 문제점이 있다.

 

• 물체의 방향을 정의하는 데 있어 오일러 각 (∂_x, ∂_y, ∂_z)는 매우 직관적인 수단을 제공한다.
• 하지만, 오일러 각이 가진 문제 중 하나는, 이것이 올바르게 보간된다는 보장이 없다는 사실이다.
• 가장 위에 있는 그림이 키프레임 0, 그 다음이 키프레임 1의 모습일 때, 이 둘을 선형보간하여 t = 0.5인 중간 프레임에서의 방향을 계산해 보면 그 결과는 (45˚, 67.5˚, 45˚)이다.
• 가장 밑의 그림은 이 오일러 각을 연속적으로 적용한 결과를 보여준다. 하지만, L자형 물체의 양 끝점의 x좌표를 보면 이들은 0이 아니다.
• 즉, 물체는 yz 평면에 놓여있지 않다. 두 키프레임의 물체가 yz평면에 놓여있기 때문에 중간 프레임의 물체도 그렇게 되어야 하는데, 오일러 각 보간은 예기치 않은 결과를 낳은 것이다.

 

• 이처럼 오일러 각은 올바르게 보간된다는 보장이 없기 때문에, 보간을 핵심 기능으로 가지는 키프레임 애니메이션에 적합하지 않다. 하지만, 쿼터니언(quaternion)은 항상 올바르게 보간된다.

 

 

 

 

 

---

 

 

 

 

 

출처

한정현 - [OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문]을 보고 공부하고 정리한 내용입니다.